Remix of Functions and Function Notation
- Read more about Remix of Functions and Function Notation
- Log in or register to post comments
- 28 views
Learning Objectives
In this section, you will:
- Determine whether a relation represents a function.
- Find the value of a function.
- Determine whether a function is one-to-one.
- Use the vertical line test to identify functions.
- Graph the functions listed in the library of functions.
A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.
Determining Whether a Relation Represents a Function
A relation is a set of ordered pairs. The set consisting of the first components of each ordered pair is called the domain and the set consisting of the second components of each ordered pair is called the range. Consider the following set of ordered pairs. The first numbers in each pair are the first five natural numbers. The second number in each pair is twice that of the first.
$$\{(1,\text{ }2),\text{ }(2,\text{ }4),\text{ }(3,\text{ }6),\text{ }(4,\text{ }8),\text{ }(5,\text{ }10)\}$$
The domain is \(\{1,\text{ }2,\text{ }3,\text{ }4,\text{ }5\}\). The range is \(\{2,\text{ }4,\text{ }6,\text{ }8,\text{ }10\}\).
Note that each value in the domain is also known as an input value, or independent variable, and is often labeled with the lowercase letter \(x\). Each value in the range is also known as an output value, or dependent variable, and is often labeled lowercase letter \(y\).
A function \(f\) is a relation that assigns a single value in the range to each value in the domain. In other words, no x-values are repeated. For our example that relates the first five natural numbers to numbers double their values, this relation is a function because each element in the domain, \(\{1, 2, 3, 4, 5\}\), is paired with exactly one element in the range, \(\{2, 4, 6, 8, 10\}\).
Now let’s consider the set of ordered pairs that relates the terms “even” and “odd” to the first five natural numbers. It would appear as
$$\{{(\text{odd},\text{ }1),\text{ }(\text{even},\text{ }2),\text{ }(\text{odd},\text{ }3),\text{ }(\text{even},\text{ }4),\text{ }(\text{odd},\text{ }5)}\}$$
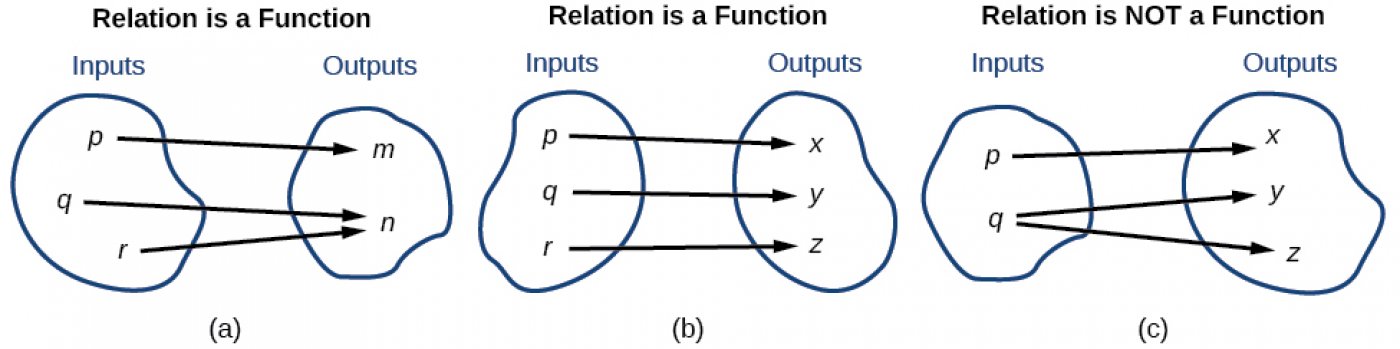
Notice that each element in the domain, \(\{even, odd\}\) is not paired with exactly one element in the range, \(\{1, 2, 3, 4, 5\}\). For example, the term “odd” corresponds to three values from the range, \(\{1, 3, 5\}\) and the term “even” corresponds to two values from the range, \(\{2, 4\}\). This violates the definition of a function, so this relation is not a function.
Figure 1 compares relations that are functions and not functions.
Functions
A function is a relation in which each possible input value leads to exactly one output value. We say “the output is a function of the input.”
The input values make up the domain, and the output values make up the range.
Examples
Given a relationship between two quantities, determine whether the relationship is a function.
Using Function Notation
Once we determine that a relationship is a function, we need to display and define the functional relationships so that we can understand and use them, and sometimes also so that we can program them into computers. There are various ways of representing functions. A standard function notation is one representation that facilitates working with functions.
To represent “height is a function of age,” we start by identifying the descriptive variables \(h\) for height and \(a\) for age. The letters \(f\), \(g\), and \(h\) are often used to represent functions just as we use \(x, y\), and \(z\) to represent numbers and \(A, B\), and \(C\) to represent sets.
$$ \begin{array}{lcccc}h\text{ is }f\text{ of }a&&&&\text{We name the function }f;\text{ height is a function of age}.\\h=f(a)&&&&\text{We use parentheses to indicate the function input}\text{. }\\f(a)&&&&\text{We name the function }f;\text{ the expression is read as “}f\text{ of }a\text{.”}\end{array} $$
Remember, we can use any letter to name the function; the notation \(h(a)\) shows us that \(h\) depends on \(a\). The value a a must be put into the function \(h\) to get a result. The parentheses indicate that age is input into the function; they do not indicate multiplication.
We can also give an algebraic expression as the input to a function. For example \(f(a+b)\) means "first add a and b, and the result is the input for the function f." The operations must be performed in this order to obtain the correct result.
Function Notation
The notation \(y=f(x)\) defines a function named \(f\). This is read as "\(y is a function of x\)". The letter \(x\) represents the input value, or independent variable. The letter \(y\), or \(f(x)\), represents the output value, or dependent variable.
Practice Quiz
Content for this page has been sourced from OpenStax - Access for free at https://openstax.org/books/algebra-and-trigonometry/pages/1-introduction-to-prerequisites

Login or register to share your adaptations.
List of adaptions
Be the first to add your adaptation here!
Login or register to engage in the review and feedback process.
Reviews and Feedback
Be the first to review!


Comments
Be the first to comment!